等比数列とは、一定の比率で変化していくような数列のことです。 このページでは、等比数列の意味、一般項の求め方、 等比数列の意味、一般項の求め方、等比数列の和など、等比数列の知識を基礎から全て解説します。. 無限等比級数は次のように収束・発散します．. となる．. 無限級数 ∑ n = 1 ∞ a n が収束するには， 少なくとも数列 { a n } が0に収束していなければならなかった ことを思い出しておきましょう．. もし等比数列 { a n } の初項が0でなければ，公比が r < − 1.
等 比 級数 公式 オイラーの公式
5分で解説 無限等比級数基礎1 YouTube
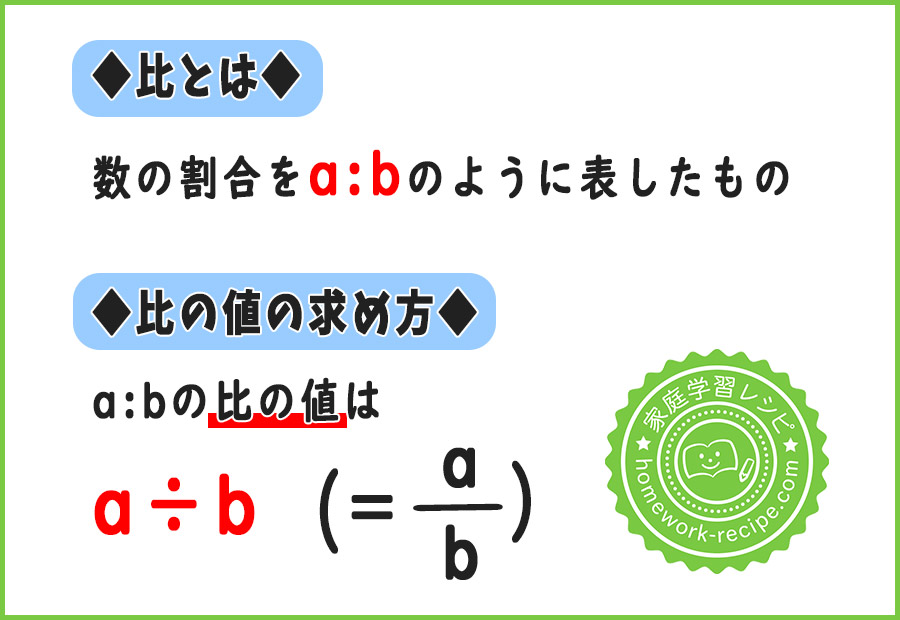
比と比の値についての自主学習ノート例 家庭学習レシピ
無限等比数列と無限等比級数で表された関数のグラフと連続性 受験の月
数列の極限と無限等比級数をわかりやすく解説！数学Ⅲ分野の苦手意識をなくそう｜高校生向け受験応援メディア「受験のミカタ」
等比数列とは？一般項の求め方や和の公式を練習問題と解説でマスターしよう！｜高校生向け受験応援メディア「受験のミカタ」
等比数列とは？一般項の求め方や和の公式を練習問題と解説でマスターしよう！｜高校生向け受験応援メディア「受験のミカタ」
等比数列の公式まとめ（一般項・和の公式・証明） 理系ラボ
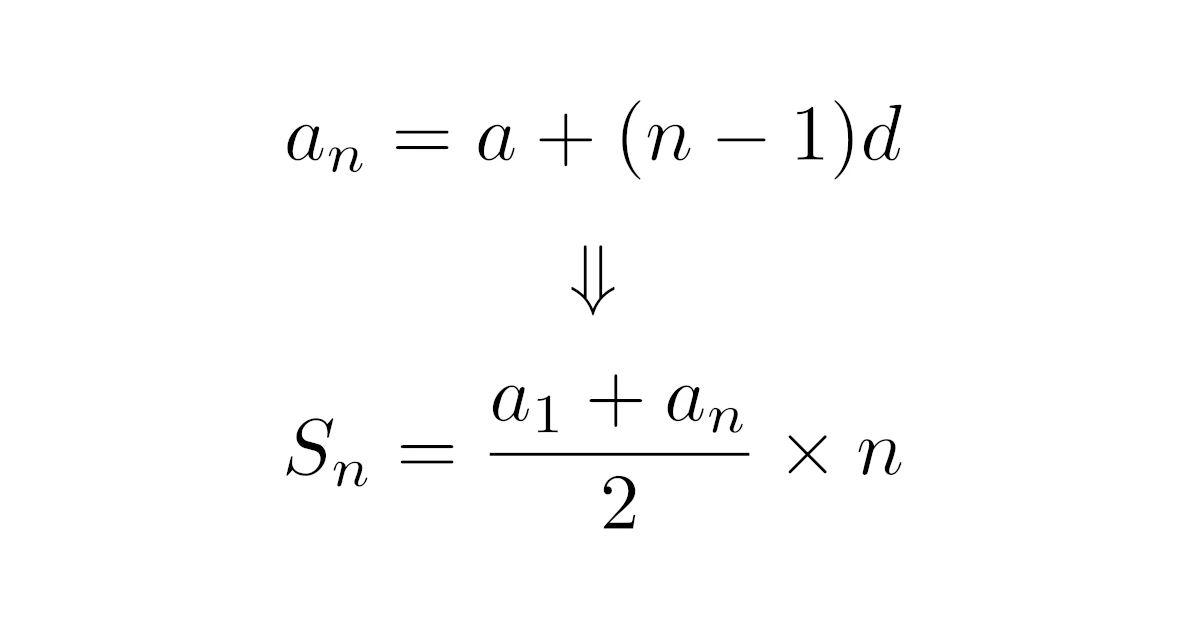
等差数列の和の公式｜直感的に理解する方法と導出 合格タクティクス
【高校数学Ⅲ】「無限等比級数（4）」(問題編) 映像授業のTry IT (トライイット)
【3分でわかる！】等比数列の一般項、等比中項、和の公式をわかりやすく 合格サプリ
無限等比級数とは？公式と条件をわかりやすく解説
数列の極限と無限等比級数をわかりやすく解説！数学Ⅲ分野の苦手意識をなくそう｜高校生向け受験応援メディア「受験のミカタ」
無限級数・無限等比級数が定義からしっかりと理解できる！ okke
![[117] 等比級数と積分の応用 面白い無限級数1 メルカトル級数の上位互換 YouTube](https://i.ytimg.com/vi/pKbOjo4RuB8/maxresdefault.jpg "[117] 等比級数と積分の応用 面白い無限級数1 メルカトル級数の上位互換 YouTube")
[117] 等比級数と積分の応用 面白い無限級数1 メルカトル級数の上位互換 YouTube
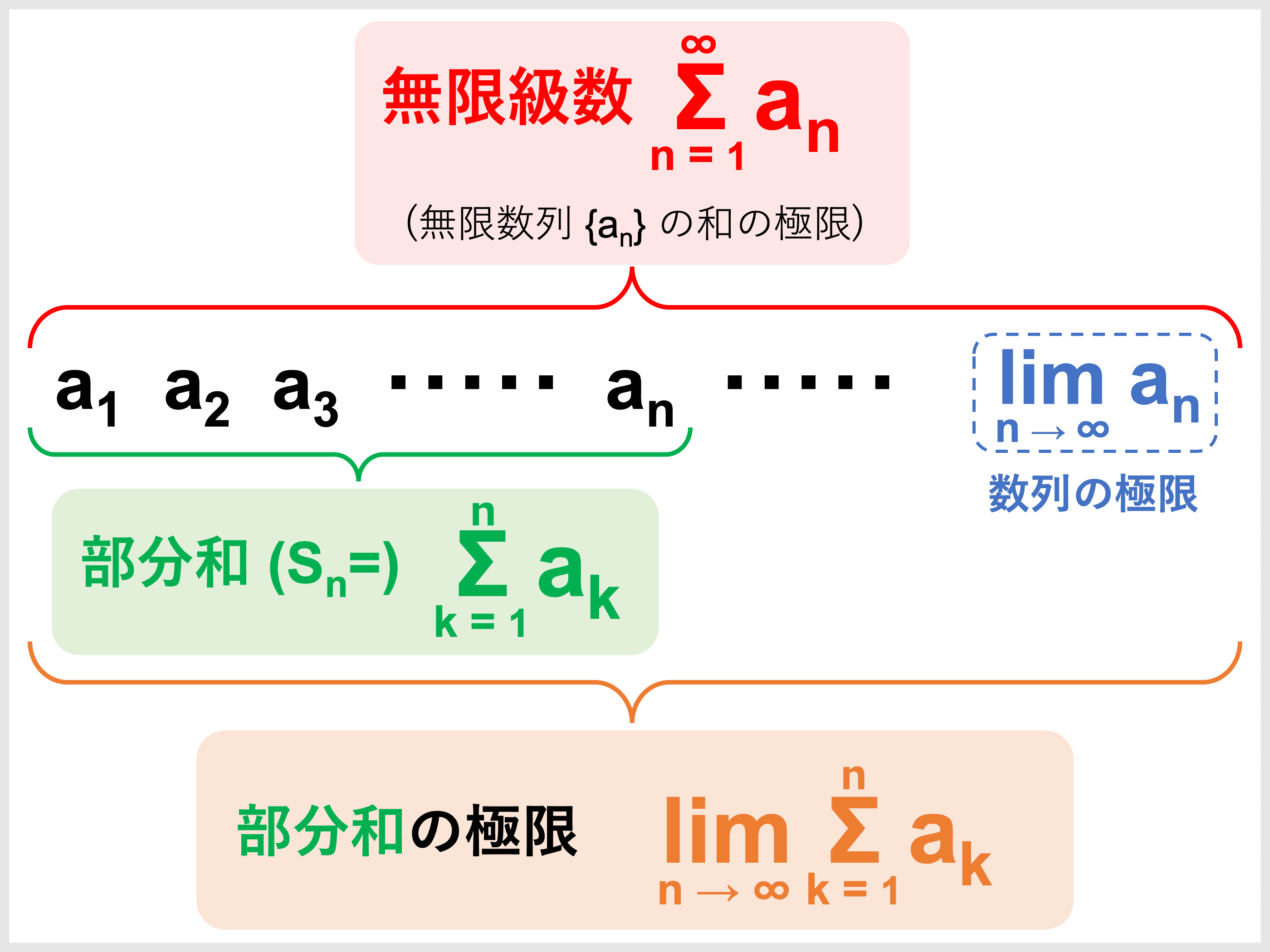
無限級数、無限等比級数とは？和の公式や求め方、図形問題 受験辞典
![等 比 数列 の 和 🤚 数列の基本2｜[等差数列の和の公式]と[等比数列の和の公式]](https://kaito.click/img/clearBK/195.png "等 比 数列 の 和 🤚 数列の基本2｜[等差数列の和の公式]と[等比数列の和の公式]")
等 比 数列 の 和 🤚 数列の基本2｜[等差数列の和の公式]と[等比数列の和の公式]
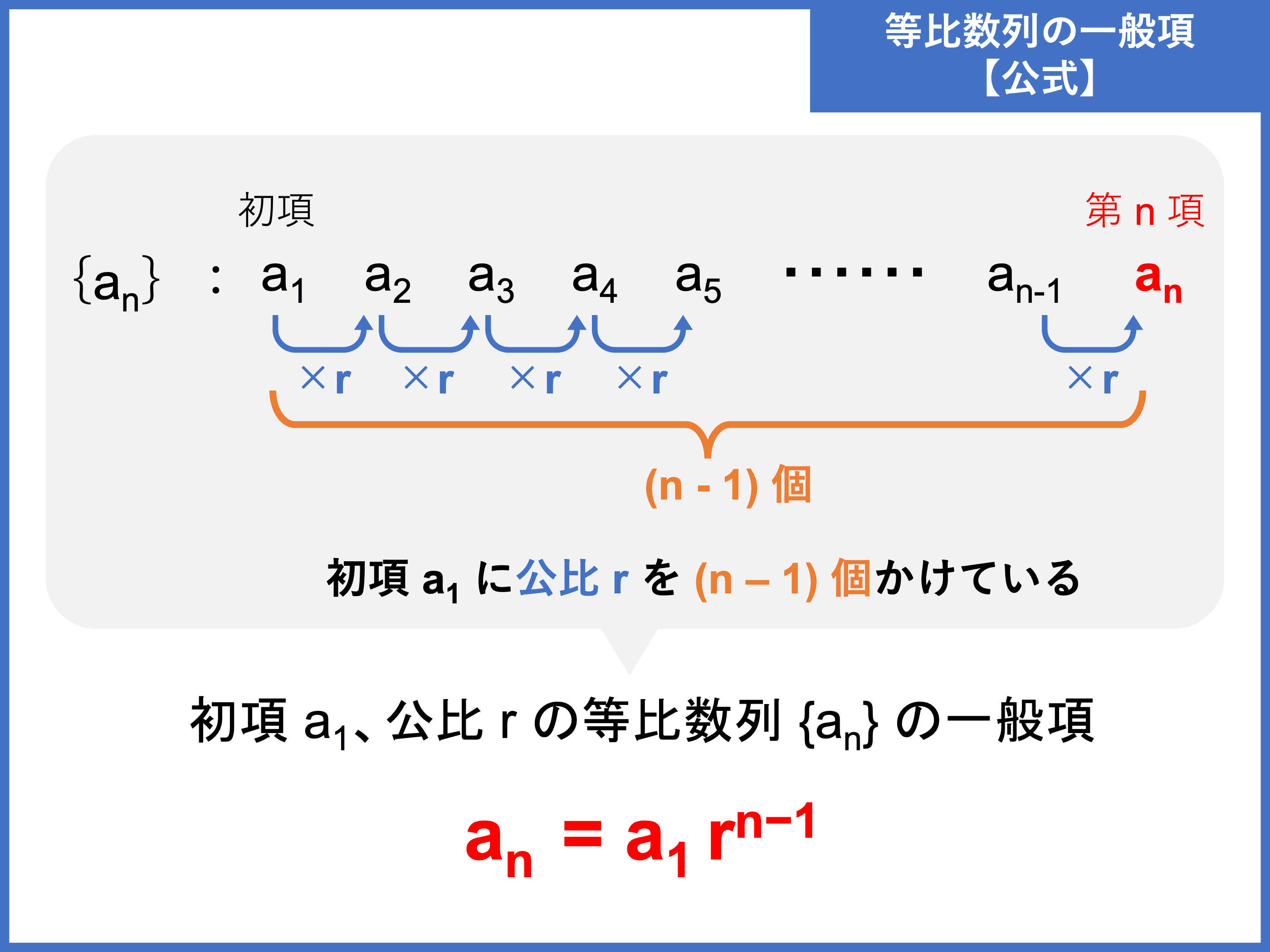
等比数列をわかりやすく解説！一般項や等比数列の和の公式 受験辞典
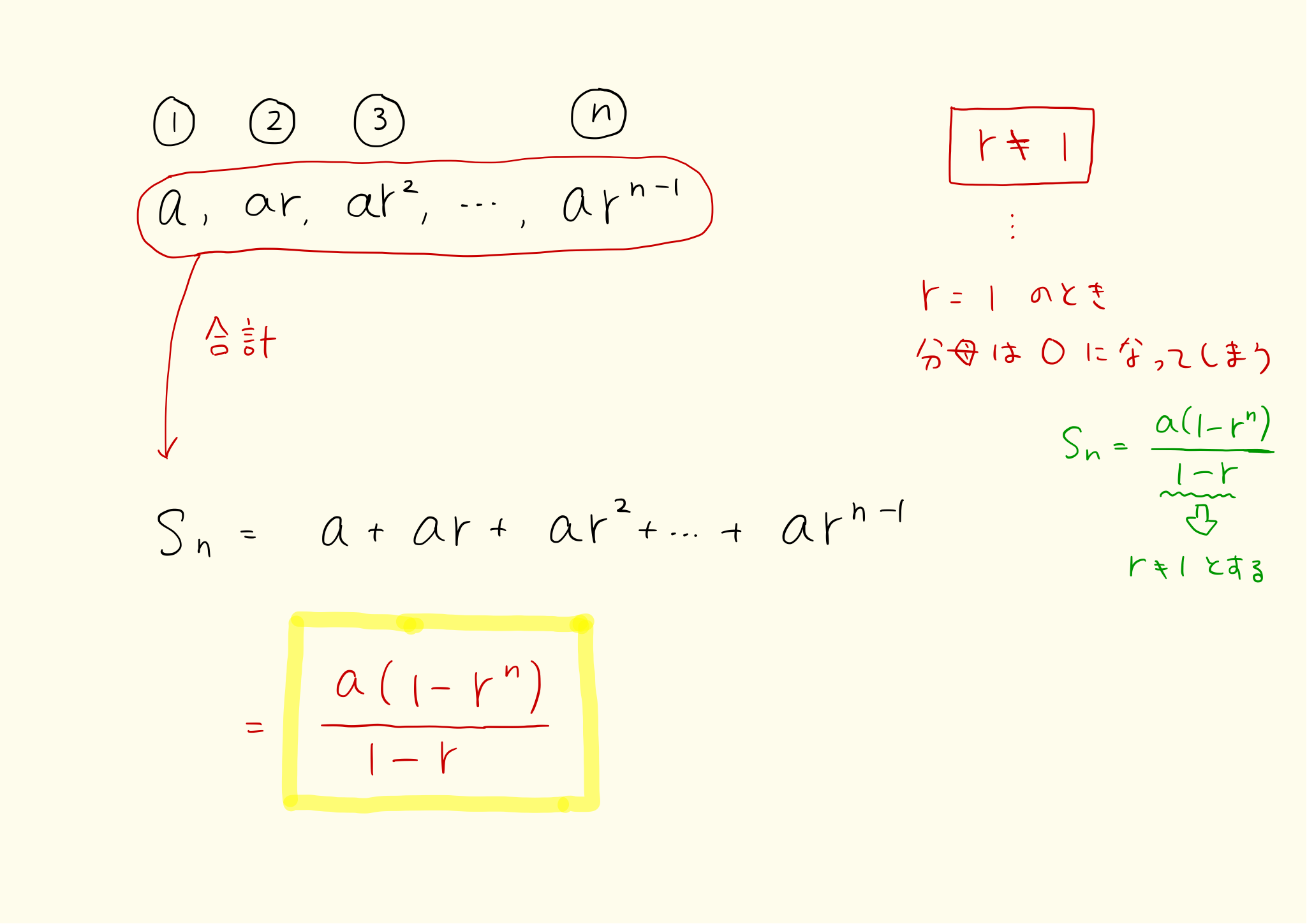
等比数列とは？等比数列の意味と性質、一般項と和の公式をわかりやすく解説 Irohabook
![等 比 数列 の 和 🤚 数列の基本2｜[等差数列の和の公式]と[等比数列の和の公式]](https://livedoor.blogimg.jp/boxeur-1102/imgs/4/e/4e510e77.jpg "等 比 数列 の 和 🤚 数列の基本2｜[等差数列の和の公式]と[等比数列の和の公式]")
等 比 数列 の 和 🤚 数列の基本2｜[等差数列の和の公式]と[等比数列の和の公式]
つまり、等比数列とは初項が であり、なおかつ隣り合う項が共通の比 を持つ数列です。. この を 公比 （common ratio）と呼びます。. 等比数列 の項の無限級数は、 となりますが、このような無限級数を 等比級数 （geometric series）と呼びます。. 例（等比級数.. 無限等比級数の和の公式の証明. 等比数列 の初項から第 項までの和 は、. のとき、 等比数列の和の公式 より. と表されます。. のとき、. 1より小さい数は、かければかけるほど小さくなるので. となります。. このとき無限等比級数の和は収束しその値は.
